For all the passionate teachers,students and mathematics enthusiasts may this be a platform to interact..
Monday, 19 November 2012
Monday, 3 September 2012
Wednesday, 29 August 2012
Monday, 27 August 2012
Monday, 13 August 2012
Number of regions...
A circle and a parabola are drawn on a sheet of paper. Find the maximum number of regions they divide the paper into.
I can see 7...can you work out and improvise?
I can see 7...can you work out and improvise?
Area of octagon...
ABCD is a square with length of a side 1 cm. An octagon is formed by lines joining the vertices of the square to the midpoints of opposite sides. Find the area of the octagon.
Answer appears to be 1/6 sq cm... try to arrive at it
Answer appears to be 1/6 sq cm... try to arrive at it
Sunday, 12 August 2012
Friday, 27 July 2012
Saturday, 17 March 2012
Area of triangle 2...
ABC is a right angled triangle with orthocentre at C. Given the circumradius as 'R' and the angle between the medians not passing through C be Ɵ. Find the area of triangle
Solution:
The Area of the triangle is

Solution:
The Area of the triangle is
Area of Triangle...
ABC is a triangle P is a point on the plane of the triangle such that |AR(PAB)| = |AR(PAC)| = |AR(PBC)|. Find possible number of positions of P.
Solution:
The answer is Four
But how...???....think !!!...let me know if you want to know
Solution:
The answer is Four
But how...???....think !!!...let me know if you want to know
Wednesday, 14 March 2012
Here follows a problem which troubles (possibly)..
... it's been days and no reply has come...so, here is the solution
consider the figure below
Let PQ be the shortest line segment such that Area of ΔCPQ is equal to Area of the Quadrilateral PQBA.
Let CP = x , CQ = y , PQ = u.
QM and BE are perpendiculars from Q and B on to CA, we can see that ΔCQM ||| ΔCBE, Then

Hence we will have QM = ysin C and BE = a sin C

PQ bisects ΔABC implies

Using the Cosine formula for triangle CPQ


Let us assume this is equal to r. then
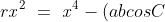\mathit{x}^{2}+\frac{a^{2}b^{2}}{4}})
Upon simplification , we get
+r}{2})^{2}+\frac{a^{2}b^{2}}{4}\ {} =\ {}\frac{(abcosC+r)^{2}}{4} })
Observation : Minimum value of R.H.S is reached when the first etrm of L.H.S is 0. ie.,
+r}{2})^{2} })
This implies that r = ab(1-cosC) and consequently we get

Therefore length of PQ can be found as
(c+a-b)}{2}} })
Generalisation:
Find a+b-c, b+c-a, c+a-b, choose the least and next higher of them; for example if a+b-c and b+c-a are these two in that order, then P and Q must be chosen on BC and BA such that

and the shortest length PQ that bisects triangle abc will then be
(b+c-a)}{2}} })
FIND THE SHORTEST LINE SEGMENT WITH ITS ENDS ON TWO SIDES OF A GIVEN TRIANGLE WHICH BISECTS THE TRIANGLE
i have a solution to this problem i will post the same however i wish someone comes out with a solution
... it's been days and no reply has come...so, here is the solution
consider the figure below
Let PQ be the shortest line segment such that Area of ΔCPQ is equal to Area of the Quadrilateral PQBA.
Let CP = x , CQ = y , PQ = u.
QM and BE are perpendiculars from Q and B on to CA, we can see that ΔCQM ||| ΔCBE, Then
Hence we will have QM = ysin C and BE = a sin C
PQ bisects ΔABC implies
Using the Cosine formula for triangle CPQ
Let us assume this is equal to r. then
Upon simplification , we get
Observation : Minimum value of R.H.S is reached when the first etrm of L.H.S is 0. ie.,
This implies that r = ab(1-cosC) and consequently we get
Therefore length of PQ can be found as
Generalisation:
Find a+b-c, b+c-a, c+a-b, choose the least and next higher of them; for example if a+b-c and b+c-a are these two in that order, then P and Q must be chosen on BC and BA such that
and the shortest length PQ that bisects triangle abc will then be
Tuesday, 10 January 2012
problem on probability
Four identical dice are rolled once, find the probability of getting atleast three different numbers.
Subscribe to:
Comments (Atom)







